Association discovery is commonly called Market Basket Analysis (MBA). MBA is widely used by grocery stores, banks, and telecommunications among others. Its results are used to optimize store layouts, design product bundles, plan coupon offers, choose appropriate specials and choose attached mailing in direct marketing. The MBA helps us to understand what items are likely to be purchased together. On-line transaction processing systems often provide the data sources for association discovery.

What is Market Basket Analysis?

People who buy Toothpaste also tend to buy a toothbrush, right? The marketing team at retail stores should target customers who buy toothpaste and toothbrush also provide an offer to them so that customer buys a third item example mouthwash. If a customer buys toothpaste and toothbrush and sees a discount offer on mouthwash they will be encouraged to spend extra and buy the mouthwash and this is what market analysis is all about. It helps us to understand what items are likely to be purchased together. On-line transaction processing systems often provide the data sources for association discovery.

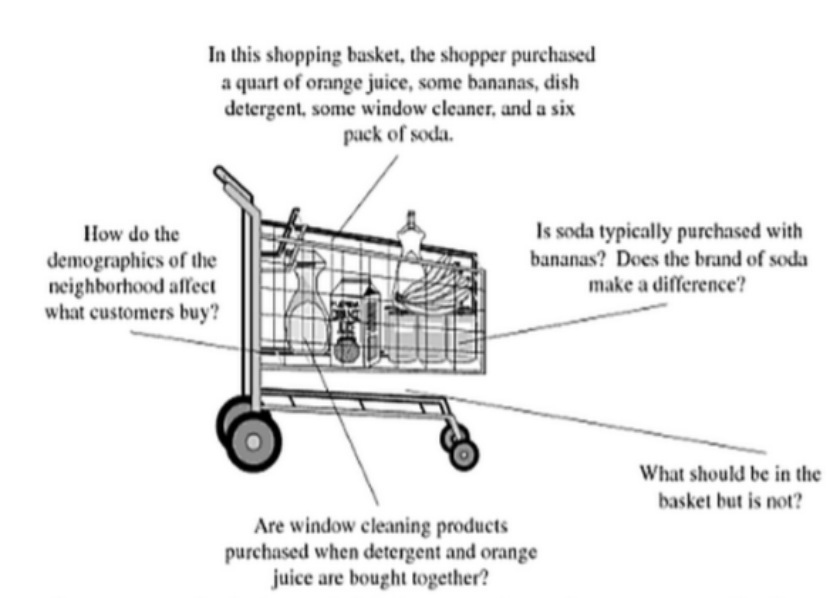
Typically, a transaction is a single customer purchase, and the items are the things that were bought. Association discovery is the identification of items that occur together in a given event or record. Association rules highlight frequent patterns of associations or causal structures among sets of items or objects in transaction databases. Association discovery rules are based on frequency counts of the number of times items occur alone and in combination in the database. They are expressed as “if item A is part of an event, then item B is also part of the event, X percent of the time.” Thus an association rule is a statement of the form (item set A) ⇒ (item set B).

Example: Customer buys toothpaste (Item A) then the chances of toothbrush (item b) being picked by the customer under the same transaction ID. One thing needs to understand here, this is not a casualty rather it is a co-occurrence pattern.

Above toothpaste is a baby example. If we take real retail stores and they have more than thousands of items. Just imagine how much revenue they can make by using this algorithm with the right placement of items. MBA is a popular algorithm that helps the business make a profit. The above A and B rule were created for two items. It is difficult to create a rule for more than 1000 items that’s where the Associate discovery and apriori algorithm comes to the picture. Let’s see how this algorithm works?

Basic Concepts for Association Discovery

An association rule is written A => B where A is the antecedent and B is the consequent. Both sides of an association rule can contain more than one item. Techniques used in Association discovery are borrowed from probability and statistics. Support, confidence, and Lift are three important evaluation criteria of association discovery.

Support

The level of support is how frequently the combination occurs in the market basket (database). Support is the percentage of baskets (or transactions) that contain both A and B of the association, i.e. % of baskets where the rule is true

Support(A => B) = P(A ∩ B)

Expected confidence

This is the probability of the consequent if it was independent of the antecedent. Expected confidence is thus the percentage of occurrences containing B

Expected confidence (A => B) = P(B)

Confidence

The strength of an association is defined by its confidence factor, which is the percentage of cases in which a consequent appears given that the antecedent has occurred. Confidence is the percentage of baskets having A that also contain B, i.e. % of baskets containing B among those containing A. Note: Confidence(A => B) ≠ Confidence(B => A).

Confidence(A => B) = P(B | A)

Lift

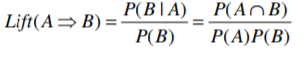
Lift is equal to the confidence factor divided by the expected confidence. Lift is a factor by which the likelihood of consequent increases given an antecedent. Expected confidence is equal to the number of consequent transactions divided by the total number of transactions. Lift is the ratio of the likelihood of finding B in a basket known to contain A, to the likelihood of finding B in any random basket.

Example: Shoes and Socks

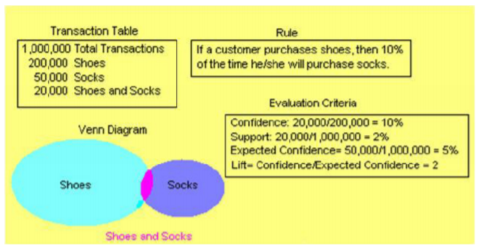
If a customer buys shoes, then 10% of the time he also buys socks.

This example rule has a left-hand side (antecedent) and a right-hand side (consequent). Shoes are the antecedent item and socks are the consequent item.

Apriori Algorithm

Apriori algorithm, a classic algorithm, is useful in mining frequent itemsets and relevant association rules. Usually, this algorithm works on a database containing a large number of transactions.

Terminology

k-itemset: a set of k items.

e.g. {beer, diapers, juice} is a 3-itemset; {cheese} is a 1-itemset; {honey, ice-cream} is a 2-itemset

Support: an itemset has support, say, 10% if 10% of the records in the database contain those items.

Minimum support: The Apriori algorithm starts a specified minimum level of support, and focuses on itemsets with at least this level.

The Apriori Algorithm, Example

Consider a lattice containing all possible combinations of only 5 products:

A = apples, B= beer, C = cider, D = diapers & E = earbuds

The Apriori algorithm is designed to operate on databases containing transactions — it initially scans and determines the frequency of individual items (i.e. the item set size, k = 1). For example, if itemset {A, B} is not frequent, then we can exclude all item set combinations that include {A, B} (see above).

A full run-through of Apriori

Step 6: To make the set of three items we need one more rule (it’s termed a self-join). It simply means, from the Item pairs in the above table, we find two pairs with the same first Alphabet, so we get OK and OE, this gives OKE, KE and KY, this gives KEY

Suppose you have sets of 3 items. For example:

ABC, ABD, ACD, ACE, BCD and we want to generate item sets of 4 items. Then, look for two sets having the same first two letters.

ABC and ABD -> ABCD , ACD and ACE -> ACDE and so on..

In general, we look for sets differing in just the last alphabet/item.

Strengths of MBA

1. Easily understood
2. Supports undirected data mining
3. Works on variable-length data records and simple computations

Weaknesses

An exponential increase in computation with a number of items (Apriori algorithm)

If you find have any feedback, please do let me know in the comments.